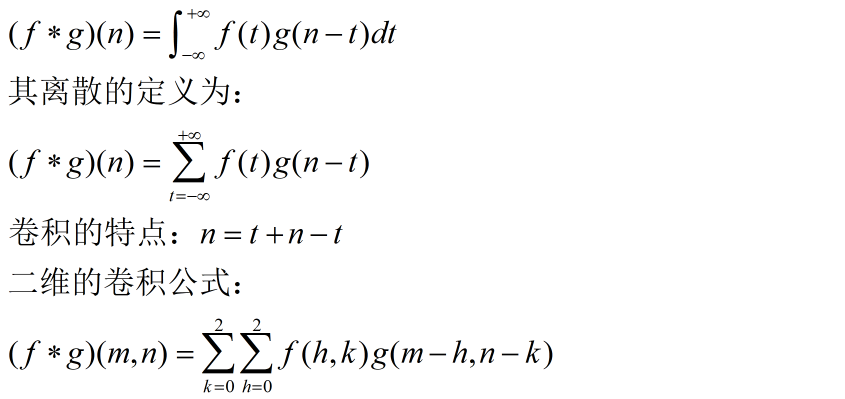Fork me on GitHub

发表于 | 分类于
字数统计: 761 | 阅读时长 ≈ 2

卷积神经网络(CNN)

​ 卷积神经网络CNN(Current Neural Network)与普通神经网络类似，它们都有可学习的权重(Weights)和偏置常量(biases)的神经元组成。每个神经元都接受一些输入，并做一些点积计算，输出是每个分类的分数，因此，普通神经网络里的一些计算技巧在CNN中依旧适用。CNN常用于计算机图像识别。

  • 普通神经网络：

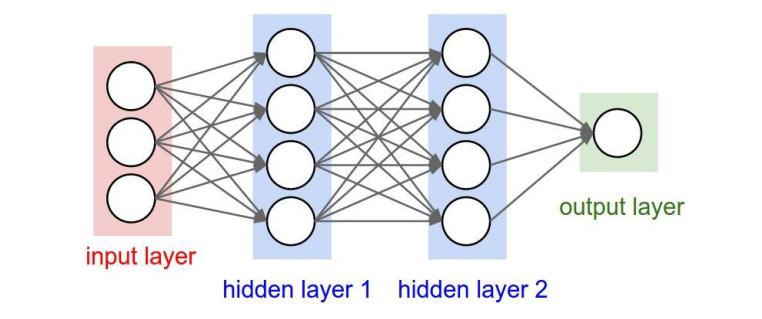
normal neural network

  • 卷积神经网络：

Current Neural Network

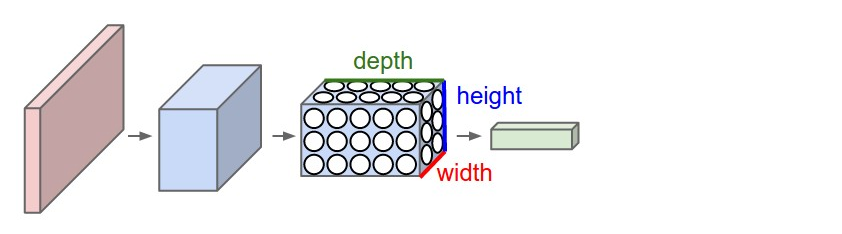
​ 卷积神经网络默认输入是图像，可以让我们把特定的性质编码编入网络结构。另外，卷积神经网络是具有三维体积的神经元。

卷积神经网络利用输入是图片的特点，把神经元设计成三个维度：width,depth,height(ps:depth不是神经网络的深度，用来描述神经元的)。

比如输入的图片大小是32323(RGB)，那么输入神经元也具有32323的维度

  • 总结：

    一个卷积神经网络由很多层组成，输入时三维的，输出也是三维的，有的层有参数，有的层不需要参数

卷积神经网络的组成

  • 卷积层(Convolutional layer)：CNN中每层卷积层由若干卷积单元组成，每个卷积单元的参数通过反向传播算法优化得到的。卷积运算的目的是提取输入的不同特征，第一层卷积可能只能提取一些低级的特征比如边缘、线条、角等层级，更多层的网络能从低级特征中迭代提取更复杂的特征。
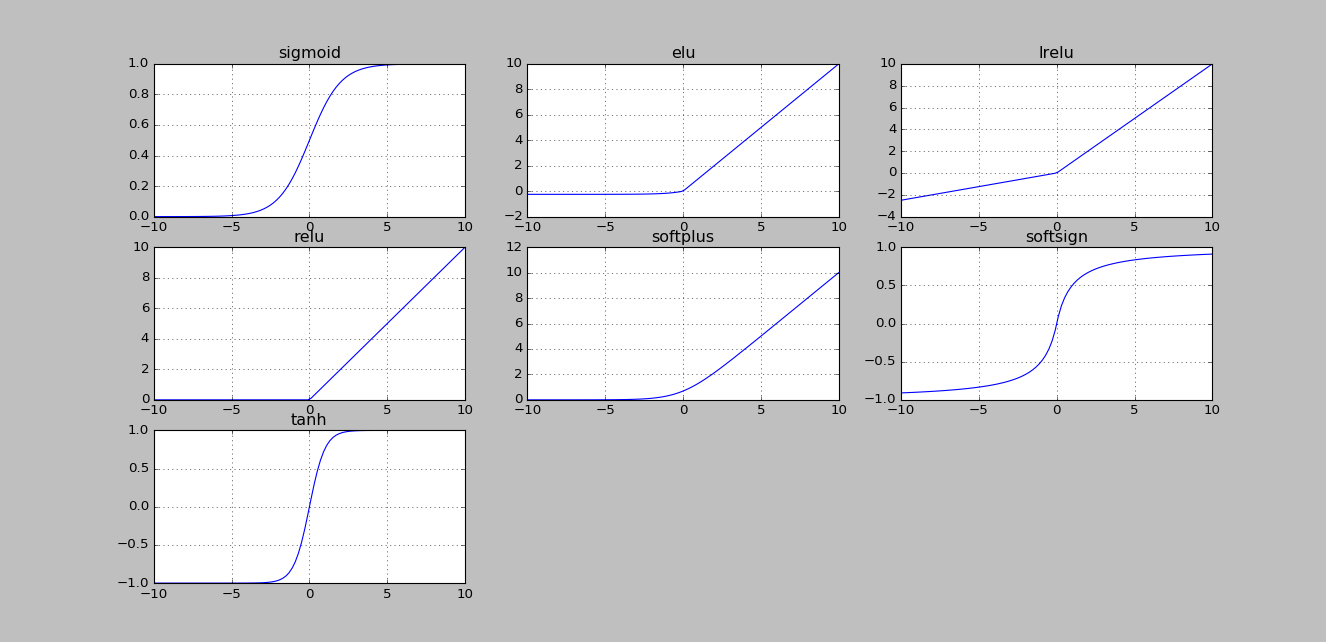
  • 线性整流层(Rectified Linear Units layer,ReLU layer):这一层是激励函数(Activation Function)，使用线性整流(Rectified Linear Units,ReLU)
  • 池化层(Pooling layer):通常在卷积层之后会得到维度很大的特征，将特征切成几个区域，取到最大值或者平均值，得到新的，维度较小的特征。
  • 全连接层(Fully-Connected layer)：把所有局部特征结合变成全局特征，用来计算最后每一类的得分。

卷积神经网络的过程：

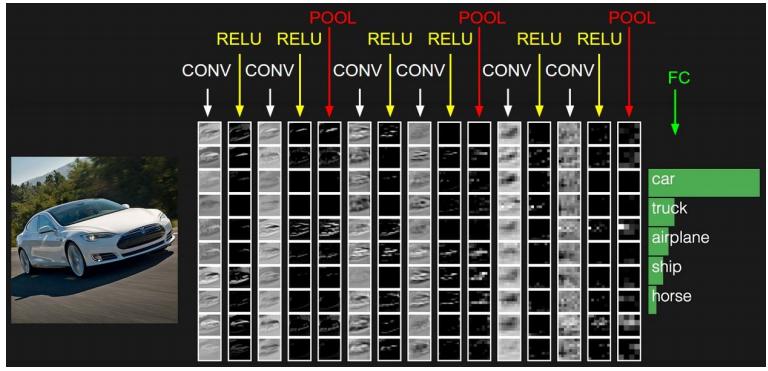
Current Neural Network

CNN的个人理解

  • CNN专门解决图像问题的，可以把它看做特征提取层，让在输入层上，最后用MLP做分类。
  • CNNs相对于MLP(Multi-Layer Perceptron,多层感知器，是最简单的DNN)，多了一个先验知识，也就是数据之间存在空间相关性。就比如图像、蓝天附近的像素点是白云的概率会大于是汽车的概率。滤波器filter会扫描整张图像，在扫描的过程中，参数共享。

σ(.)

σ(.)

σ(.)

σ(.)

σ(.)

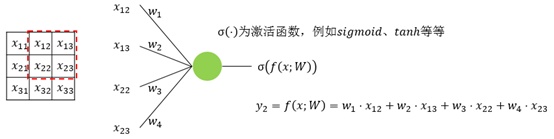
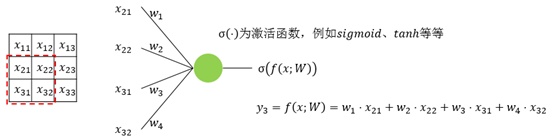
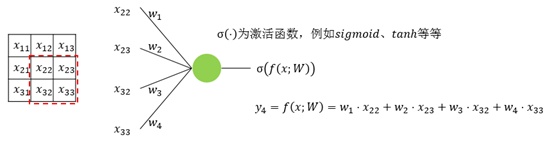
上面4附图，都是一个33的输入经过一个22的conv卷积层的过程。该卷积层conv的strides是1，padding为0

注：参数strides,padding分别决定了卷积conv操作中滑动步长和图像边沿填充方式。

  • 输出的结果为：

σ(.)

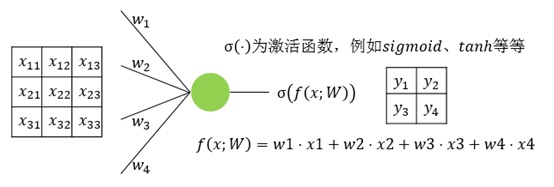
卷积的理解

学过概率论都知道有卷积公式吧。

  • 卷积公式：

卷积

发表于 | 分类于
字数统计: 418 | 阅读时长 ≈ 2 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#Classficiation分类学习
#author:victor

#MNIST数据集入门
from __future__ import print_function
import tensorflow as tf

# number 1 to 10 data
#use mnist data
#使用这两句，会在程序储存的位置出现文件夹MINIST_data
#下载MNIST数据集中的四个压缩包，并放在MINIST_data文件夹中，不要解压
#官网下载地址：http://yann.lecun.com/exdb/mnist/
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('MNIST_data/', one_hot=True)

#define add_layer function
def add_layer(inputs, in_size, out_size, activation_function=None,):
    # add one more layer and return the output of this layer
    Weights = tf.Variable(tf.random_normal([in_size, out_size]))
    biases = tf.Variable(tf.zeros([1, out_size]) + 0.1,)
    Wx_plus_b = tf.matmul(inputs, Weights) + biases
    if activation_function is None:
        outputs = Wx_plus_b
    else:
        outputs = activation_function(Wx_plus_b,)
    return outputs


#define compute_accuracy function
def compute_accuracy(v_xs, v_ys):
    global prediction
    y_pre = sess.run(prediction, feed_dict={xs: v_xs})
    correct_prediction = tf.equal(tf.argmax(y_pre,1), tf.argmax(v_ys,1))
    accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
    result = sess.run(accuracy, feed_dict={xs: v_xs, ys: v_ys})
    #output result which is the percent，this percent too high,the prediction too accurate
    return result

# define placeholder for inputs to network
xs = tf.placeholder(tf.float32, [None, 784]) # 28x28,也就是有784个数据点
ys = tf.placeholder(tf.float32, [None, 10])#有10个输出

# add output layer
prediction = add_layer(xs, 784, 10,  activation_function=tf.nn.softmax)

# the error between prediction and real data
#分类的话，用softmax配上cross_entropy(交叉熵)
cross_entropy = tf.reduce_mean(-tf.reduce_sum(ys * tf.log(prediction),
                                              reduction_indices=[1]))# loss
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)

sess = tf.Session()
# important step
# tf.initialize_all_variables() no long valid from
# 2017-03-02 if using tensorflow >= 0.12
if int((tf.__version__).split('.')[1]) < 12 and int((tf.__version__).split('.')[0]) < 1:
    init = tf.initialize_all_variables()
else:
    init = tf.global_variables_initializer()
sess.run(init)

#display the graph
for i in range(1000):
    batch_xs, batch_ys = mnist.train.next_batch(100)
    sess.run(train_step, feed_dict={xs: batch_xs, ys: batch_ys})
    if i % 50 == 0:
        print(compute_accuracy(
            mnist.test.images, mnist.test.labels))

运行效果

MNIST data result

可以看出图片识别分类的精确度并不是很高，后续用到了CNN卷积神经网络，精确度可以达到99%

发表于 | 分类于
字数统计: 517 | 阅读时长 ≈ 1

MNIST数据集简介

MNIST(Mixed National Institute of Standards and Technology database)是一个计算机视觉数据集，它包含70000张手写数字的灰度图片，其中每张图片包含28*28个像素点。可以用一个数字数组来表示这张图片。

MNIST Matrix

每张图片都有对应的标签，也就是图片对应的数字，例如上图的标签是1

数据集被分成两部分：60000行的训练数据集(mnist.train)和10000行的测试数据集(mnist.test)

其中：60000行的训练集拆分为55000行的训练集和5000行的验证集

60000行的训练数据集是一个形状为[60000,784]的张量，第一个维度数字用来表示图片索引，第二个维度的数字用来索引每张图片中的像素点。在[60000,784]的张量里的每一个元素，都表示每张图片里的某个像素的强度值，值在0，1之间。

mnist-train-xs

60000行的训练数据集标签是在0到9的数字，用来描述给定图片里表示的数字，叫做“one-hot vectors”。一个one-hot向量除了某一位的数字是1以外，其余各维度数字都是0，也就是数字n将表示成一个只有在第n维度(从0开始)数字为1的10维度向量。比如，标签0将表示成[1,0,0,0,0,0,0,0,0,0]，而标签0是一个[60000,10]的数字矩阵

mnist-train-ys

在TensorFlow里面可以用如下代码导入MNIST数据集：

1
2
3
from tensorflow.examples.tutorials.mnist import input_data

mnist=input_data.read_data_sets("MNIST_data/",one-hot=True)

引入这两句，会自动在代码文件的路径上创建一个MNIST_data文件夹。

比较烦人的是使用tensorflow.examples.tutorials.mnist import input_data读取数据的时候，经常出现网络连接超时。

解决方法：查看input_data.py

input_data

这段代码，会先检查文件是否存在，如果不存在才进行下载，我们可以自己动手下载MNIST数据。

官网下载地址：MNIST data

注：下载好数据集不要解压。

发表于 | 分类于
字数统计: 523 | 阅读时长 ≈ 2 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
#author:victor
#import module
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
tf.reset_default_graph()

#当你的模型没办法收敛的时候，可以调低学习率
"""
Tensorflow的用途，为模型，公式调参，神经网络就是用梯度下降，而
梯度下降就是一种优化模式，可以利用梯度下降机制来调参。

一般在初始化神经网络的参数时，我们可以用到Normal distribution正太分布等方式
并且多做几次初始化实验，看看效果如何，运气好的时候很成功
可以带来比较好的局部最优解。
"""
#initialize parameters
LR = 0.1
REAL_PARAMS = [1.2, 2.5]
INIT_PARAMS = [[5, 4],
               [5, 1],
               [2, 4.5]][2]

x = np.linspace(-1, 1, 200, dtype=np.float32)   # x data

# Test (1): Visualize a simple linear function with two parameters,
# you can change LR to 1 to see the different pattern in gradient descent.

#y_fun = lambda a, b: a * x + b
#tf_y_fun = lambda a, b: a * x + b


# Test (2): Using Tensorflow as a calibrating tool for empirical formula like following.

#y_fun = lambda a, b: a * x**3 + b * x**2
#tf_y_fun = lambda a, b: a * x**3 + b * x**2


# Test (3): Most simplest two parameters and two layers Neural Net, and their local & global minimum,
# you can try different INIT_PARAMS set to visualize the gradient descent.

y_fun = lambda a, b: np.sin(b*np.cos(a*x))
tf_y_fun = lambda a, b: tf.sin(b*tf.cos(a*x))

noise = np.random.randn(200)/10
y = y_fun(*REAL_PARAMS) + noise         # target

# tensorflow graph
a, b = [tf.Variable(initial_value=p, dtype=tf.float32) for p in INIT_PARAMS]
pred = tf_y_fun(a, b)
mse = tf.reduce_mean(tf.square(y-pred))
train_op = tf.train.GradientDescentOptimizer(LR).minimize(mse)

a_list, b_list, cost_list = [], [], []
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for t in range(400):
        a_, b_, mse_ = sess.run([a, b, mse])
        a_list.append(a_); b_list.append(b_); cost_list.append(mse_)    # record parameter changes
        result, _ = sess.run([pred, train_op])                          # training


# visualization codes:
print('a=', a_, 'b=', b_)
plt.figure(1)
plt.scatter(x, y, c='b')    # plot data
plt.plot(x, result, 'r-', lw=2)   # plot line fitting
# 3D cost figure
fig = plt.figure(2); ax = Axes3D(fig)
a3D, b3D = np.meshgrid(np.linspace(-2, 7, 30), np.linspace(-2, 7, 30))  # parameter space
cost3D = np.array([np.mean(np.square(y_fun(a_, b_) - y)) for a_, b_ in zip(a3D.flatten(), b3D.flatten())]).reshape(a3D.shape)
ax.plot_surface(a3D, b3D, cost3D, rstride=1, cstride=1, cmap=plt.get_cmap('rainbow'), alpha=0.5)
ax.scatter(a_list[0], b_list[0], zs=cost_list[0], s=300, c='r')  # initial parameter place
ax.set_xlabel('a'); ax.set_ylabel('b')
ax.plot(a_list, b_list, zs=cost_list, zdir='z', c='r', lw=3)    # plot 3D gradient descent
plt.show()

运行效果

Visualize-Gradient-Descent

发表于 | 分类于
字数统计: 282 | 阅读时长 ≈ 1 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#author:victor
#import module
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import math

#define a add_layer function
def add_layer(inputs, in_size, out_size, activation_function=None):
    # add one more layer and return the output of this layer
    Weights = tf.Variable(tf.random_normal([in_size, out_size]))
    biases = tf.Variable(tf.zeros([1, out_size]))
    Wx_plus_b = tf.matmul(inputs, Weights) + biases
    if activation_function is None:
        outputs = Wx_plus_b
    else:
        outputs = activation_function(Wx_plus_b)
    return outputs
 
# Make up some real data
x_data = np.linspace(-np.pi,np.pi,300)[:, np.newaxis]
noise = np.random.normal(0, 0.05, x_data.shape)
y_data = np.sin(x_data) + noise
 
# define placeholder for inputs to network
xs = tf.placeholder(tf.float32, [None, 1])
ys = tf.placeholder(tf.float32, [None, 1])
# add hidden layer
l1 = add_layer(xs, 1, 10, activation_function=tf.nn.relu)
# add output layer
prediction = add_layer(l1, 10, 1, activation_function=tf.nn.tanh)
 
loss = tf.reduce_mean(tf.square(ys - prediction))
train_step = tf.train.GradientDescentOptimizer(0.05).minimize(loss)
 
init = tf.initialize_all_variables()
sess = tf.Session()
sess.run(init)
 
# plot the real data
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.scatter(x_data, y_data)
# Interactive mode on
plt.ion()
plt.show()
 
for i in range(5000):
    # training
    sess.run(train_step, feed_dict={xs: x_data, ys: y_data})
    if i % 50 == 0:
        # to visualize the result and remove the previous line 
        try:
            #ax.lines.remove(lines[0])             
            #每次抹除线，先暂停0.1秒
             plt.pause(0.1)
             ax.lines.remove(lines[0])  #在图片中，去除掉第一个线段
        except Exception:
            pass
        prediction_value = sess.run(prediction, feed_dict={xs: x_data})
        # plot the prediction
        lines = ax.plot(x_data, prediction_value, 'r-', lw=5)
        plt.pause(0.1)

运行效果

batch gradient descent sinx

发表于 | 分类于
字数统计: 484 | 阅读时长 ≈ 2

用Batch Gradient Descent来拟合二次函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#批量梯度下降算法
#author:victor

#import module
import tensorflow as tf
import numpy as np

#输出结果可视化模块
import matplotlib.pyplot as plt
#定义一个添加神经层的函数
def add_layer(inputs,in_size,out_size,activation_function=None):
    Weights=tf.Variable(tf.random_normal([in_size,out_size]))
    biases=tf.Variable(tf.zeros([1,out_size])+0.1)#因为biases（偏差）推荐值不能为0，所以加上一个0.1
    #Wx_plus_b=tf.matmul(inputs,Weights)+biases#inputs+Weights+biases
    Wx_plus_b=tf.add(tf.matmul(inputs,Weights),biases)
    if activation_function is None:
        outputs=Wx_plus_b
    else:
        outputs=activation_function(Wx_plus_b)
    return outputs

x_data=np.linspace(-1,1,300)[:,np.newaxis]#（-1,1）区间的生成300个数等差数列，np.newaxis定义格式为300个行
#define a noise，定义一个噪声，来让它不是正规的二次函数。
noise=np.random.normal(0,0.05,x_data.shape)#定义跟x_data数据一样的格式
#真实值
y_data=np.square(x_data)-0.5+noise#这个是拟合函数y=x^2+nosie
#placeholder用来参数
xs=tf.placeholder(tf.float32,[None,1])
ys=tf.placeholder(tf.float32,[None,1])
#隐藏层随便有多少个神经元，越少，越差，先定义一个
l1=add_layer(xs,1,10,activation_function=tf.nn.relu)
#预测值
prediction=add_layer(l1,10,1,activation_function=None)
#误差
loss=tf.reduce_mean(tf.reduce_sum(tf.square(ys-prediction),
                   reduction_indices=[1]))
train_step=tf.train.GradientDescentOptimizer(0.1).minimize(loss)#GradientDescentOptimizer给定一个learning rate,通常是小于1
#must step,初始化变量
init=tf.initialize_all_variables()

with tf.Session() as sess:
    sess.run(init)
    #显示图形
    fig=plt.figure()
    ax=fig.add_subplot(1,1,1)
    ax.scatter(x_data,y_data)
    plt.ion()#就是让图片show了后不用暂停
    plt.show()
    
    for i in range(1000):#执行1000次
        sess.run(train_step,feed_dict={xs:x_data,ys:y_data})#只用通过placeholder的，都要用feed_dict传参数
        if i%50:                  
            #to see the step improvement控制台看，每一步的误差减少
            #print(sess.run(loss,feed_dict={xs:x_data,ys:y_data}))            
            try:  
                #预测值
                prediction_value=sess.run(prediction,feed_dict={xs:x_data})
                lines=ax.plot(x_data,prediction_value,'r-',lw=5)             
                #每次抹除线，先暂停0.1秒
                plt.pause(0.1)
                ax.lines.remove(lines[0])  #在图片中，去除掉第一个线段
            except Exception:
                pass

运行效果

batch gradient descent

发表于 | 分类于
字数统计: 428 | 阅读时长 ≈ 2 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
#为什么需要激励函数？Why need activation function?
#激励函数就是为了解决不能用线性方程(Linear)解决的问题，y=w*x+b。也就是非线性方程问题(Nonlinear)
#y=Wx-->y=AF(Wx)
#一些常用的AF非线性函数,比如relu，sigmoid，tanh，也就是激励函数
#relu为，x>0,f(x)=1,x<=0,f(x=0)
#你也可以自己创建自己的激励函数，但是函数必须保证是可微分的
#在卷积神经网络中，推荐使用relu激励函数
#在循环神经网络中(Recurrent Nerual Network)推荐适用relu or tanh
#sigmoid函数，也叫Logistics会出现梯度消失
import numpy as np
import matplotlib.pyplot as plt


def sigmoid(x):
    y = 1.0 / (1.0 + np.exp(-x))
    return y


def elu(x, a):
    y = x.copy()
    for i in range(y.shape[0]):
        if y[i] < 0:
            y[i] = a * (np.exp(y[i]) - 1)
    return y


def lrelu(x, a):
    y = x.copy()
    for i in range(y.shape[0]):
        if y[i] < 0:
            y[i] = a * y[i]
    return y


def relu(x):
    y = x.copy()
    y[y < 0] = 0
    return y


def softplus(x):
    y = np.log(np.exp(x) + 1)
    return y


def softsign(x):
    y = x / (np.abs(x) + 1)
    return y


def tanh(x):
    y = (1.0 - np.exp(-2 * x)) / (1.0 + np.exp(-2 * x))
    return y

#invoke this function
x = np.linspace(start=-10, stop=10, num=100)
y_sigmoid = sigmoid(x)
y_elu = elu(x, 0.25)
y_lrelu = lrelu(x, 0.25)
y_relu = relu(x)
y_softplus = softplus(x)
y_softsign = softsign(x)
y_tanh = tanh(x)

tx = 6
ty = 0.9

#display the graph
plt.subplot(331)
plt.title('sigmoid')
plt.plot(x, y_sigmoid)
plt.grid(True)
plt.subplot(332)
plt.title('elu')
plt.plot(x, y_elu)
plt.grid(True)
plt.subplot(333)
plt.title('lrelu')
plt.plot(x, y_lrelu)
plt.grid(True)
plt.subplot(334)
plt.title('relu')
plt.plot(x, y_relu)
plt.grid(True)
plt.subplot(335)
plt.title('softplus')
plt.plot(x, y_softplus)
plt.grid(True)
plt.subplot(336)
plt.title('softsign')
plt.plot(x, y_softsign)
plt.grid(True)
plt.subplot(337)
plt.title('tanh')
plt.plot(x, y_tanh)
plt.grid(True)
plt.show()

Activatoin Function

发表于 | 分类于
字数统计: 859 | 阅读时长 ≈ 4

线性回归(Linear Regression）

  • 线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。其表达形式为y = w’x+e，e为误差服从均值为0的正态分布
  • 回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。
  • 梯度下降是用于找到函数最小值的一阶迭代优化算法。为了使用梯度下降找到函数的局部最小值，需要采用与当前点处函数的梯度（或近似梯度）的负值成比例的步长。相反，如果采用与梯度的正值成比例的步长，则接近该函数的局部最大值 ; 然后将该过程称为梯度上升。

废话不多说，直接上代码，展示运行效果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
#Linear Regression线性回归
#author:victor
from future import print_function
import tensorflow as tf
import numpy
import matplotlib.pyplot as plt

#generate number
rng = numpy.random

# Parameters
learning_rate = 0.01
training_epochs = 1000
display_step = 50

# Training Data
#numpy.asarray和array都可以讲结构数据转化为ndarray
#区别：当数据源是ndarray时，array仍然会copy出一个副本，占用新的内存，#但是asarray不会
train_X = numpy.asarray([3.3,4.4,5.5,6.71,6.93,4.168,9.779,6.182,7.59,2.167,
                         7.042,10.791,5.313,7.997,5.654,9.27,3.1])
train_Y = numpy.asarray([1.7,2.76,2.09,3.19,1.694,1.573,3.366,2.596,2.53,1.221,
                         2.827,3.465,1.65,2.904,2.42,2.94,1.3])

n_samples = train_X.shape[0]


# tf Graph Input
X = tf.placeholder("float")
Y = tf.placeholder("float")

# Set model weights
W = tf.Variable(rng.randn(), name="weight")
b = tf.Variable(rng.randn(), name="bias")

# Construct a linear model
pred = tf.add(tf.multiply(X, W), b)

# Mean squared error
cost = tf.reduce_sum(tf.pow(pred-Y, 2))/(2*n_samples)

# Gradient descent
#  Note, minimize() knows to modify W and b because Variable objects are #trainable=True by default

#优化器，采用梯度下降方法来训练学习
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)

# Initialize the variables (i.e. assign their default value)
init = tf.global_variables_initializer()

# Start training
with tf.Session() as sess:
    # Run the initializer
    sess.run(init)

    # Fit all training data
    for epoch in range(training_epochs):
        for (x, y) in zip(train_X, train_Y):
            sess.run(optimizer, feed_dict={X: x, Y: y})


        # Display logs per epoch step(控制台显示每次步骤)
        if (epoch+1) % display_step == 0:
            c = sess.run(cost, feed_dict={X: train_X, Y:train_Y})
            print("Epoch:", '%04d' % (epoch+1), "cost=", "{:.9f}".format(c), \
                "W=", sess.run(W), "b=", sess.run(b))

    print("Optimization Finished!")
    training_cost = sess.run(cost, feed_dict={X: train_X, Y: train_Y})
    print("Training cost=", training_cost, "W=", sess.run(W), "b=", sess.run(b), '\n')



    # Graphic display(图像展示）the original data on the graph
    plt.plot(train_X, train_Y, 'ro', label='Original data')
    plt.plot(train_X, sess.run(W) * train_X + sess.run(b), label='Fitted line')
    plt.legend()
    plt.show()


    # Testing example, as requested (Issue #2)
    test_X = numpy.asarray([6.83, 4.668, 8.9, 7.91, 5.7, 8.7, 3.1, 2.1])
    test_Y = numpy.asarray([1.84, 2.273, 3.2, 2.831, 2.92, 3.24, 1.35, 1.03])

    print("Testing... (Mean square loss Comparison)")

    testing_cost = sess.run(
        tf.reduce_sum(tf.pow(pred - Y, 2)) / (2 * test_X.shape[0]),
        feed_dict={X: test_X, Y: test_Y})  # same function as cost above

    print("Testing cost=", testing_cost)
    print("Absolute mean square loss difference:", abs(
        training_cost - testing_cost))


	#display the Test data on the graph
    plt.plot(test_X, test_Y, 'bo', label='Testing data')
    plt.plot(train_X, sess.run(W) * train_X + sess.run(b), label='Fitted line')
    plt.legend()
    plt.show()

控制台的每一次梯度下降后的误差值：

Linear Regression

线性回归后的结果图展示：

Linear Regression

发表于 | 分类于
字数统计: 142 | 阅读时长 ≈ 1

画Sinx函数图像

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#正弦函数图像
#author:victor

#import module
import numpy as np
import matplotlib.pyplot as plt

#generate number
x=np.arange(0,2*np.pi,0.00001)
y=np.sin(x)

#display the graph
plt.plot(x,y)
plt.show()

sinx

画cosx/x的图像

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#画出cosx/x的图像
#author:victor

#import module
import numpy as np
import matplotlib.pyplot as plt

#define function
def f(x):
    return np.cos(x*30)/x

#generate number
g=np.frompyfunc(f,1,1)
a=np.arange(0.1,2*np.pi,0.00001)

#use the function
d=g(a)

#set maxsize
d_max=np.max(d)
#set minsize
d_min=np.min(d)

#display the graph
plt.figure(figsize=(52,23.65))
plt.xlim((-0.1,2*np.pi+0.1))
plt.ylim((-5,5))
plt.plot(a,d,'-',c='g',lw=2)
plt.show()

cosx/x

发表于 | 分类于
字数统计: 48 | 阅读时长 ≈ 1 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#箱型图
#author:victor

#import module
import numpy as np
import matplotlib.pyplot as plt

#normal distribution
data=np.random.normal(loc=0,scale=1,size=1000)

#sym点的形状，whis虚线的长度
plt.boxplot(data,sym='o',whis=1.5)

#display the graph
plt.show()

box